Although artistic appeal might depend on personal preference, our capacity to recognize trees within artistic works might relate to objective—and relatively straightforward—mathematics, as suggested by a recent investigation.

Conducted by scholars from the University of Michigan and the University of New Mexico, the research explored how the relative thickness of a tree’s branches influenced its tree-like representation.

This notion has been explored for centuries by artists, including Leonardo DaVinci, yet the researchers incorporated a contemporary aspect of mathematics to uncover profound understandings.

“Certain features of the artwork may seem aesthetic or subjective, but we can articulate them using mathematics,” stated Jingyi Gao, the primary author of the research. “I believe that’s quite fascinating.”

Gao undertook the study as an undergraduate in the U-M Department of Mathematics, collaborating with Mitchell Newberry, now a research assistant professor at UNM and an affiliate of the U-M Center for the Study of Complex Systems. Gao is currently pursuing doctoral studies at the University of Wisconsin.

The researchers specifically discovered a particular value linked to the complexity and proportions of a tree’s branches that artists have modified and manipulated to influence whether and how observers interpret a tree.

“We’ve developed a concept that universally applies to all trees in both art and nature,” claimed Newberry, the senior author of the study. “It lies at the heart of numerous representations of trees, irrespective of their diverse styles, cultures, or historical periods.”

The findings are published in the journal PNAS Nexus.

Regarding fractals

The mathematics employed by the duo to tackle their issue of proportions is grounded in fractals. In geometric terms, fractals are constructs that replicate the same designs at varying scales.

Fractals are referenced in the Oscar-winning smash hit “Let it Go” from Disney’s “Frozen,” making it challenging to dispute that there’s a more popular tangible illustration than the self-replicating crystal forms of snowflakes. Nevertheless, biology also abounds with essential fractals, including the branching architectures of lungs, blood vessels, and, of course, trees.

“Fractals are simply shapes that repeat,” Gao explained. “If you observe a tree, its branches exhibit branching. Subsequently, the smaller branches mimic the figure of the larger parent branch.”

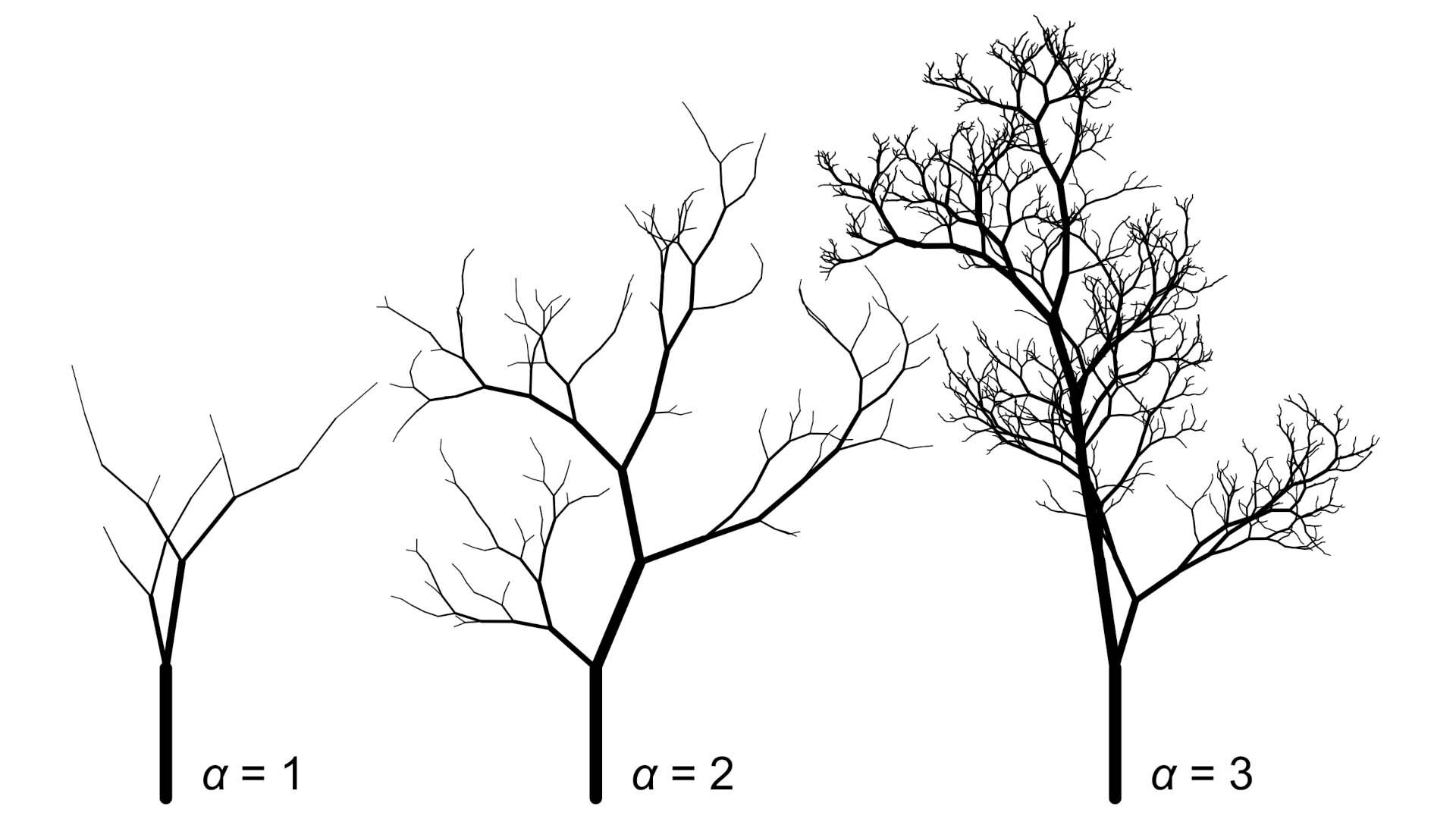
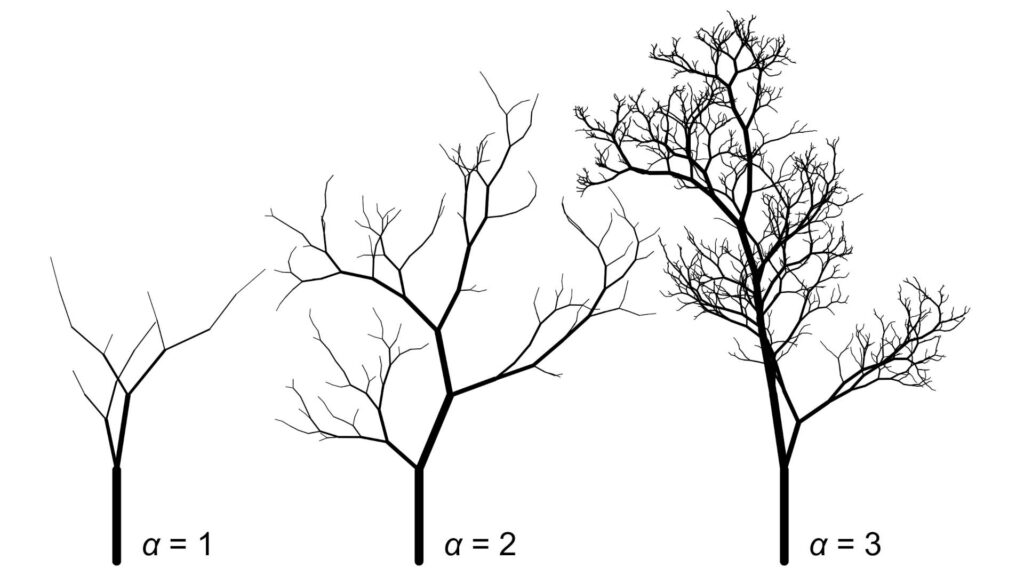
In the later part of the 20th century, mathematicians introduced a measure known as fractal dimension to quantify the intricacy of a fractal. In their investigation, Gao and Newberry analyzed a similar measure for tree branches, referred to as the branch diameter scaling exponent. This scaling factors the variation in branch diameter by assessing how many smaller branches exist per larger branch.

“We assess branch diameter scaling in trees, which fulfills the same role as the fractal dimension,” Newberry stated. “It illustrates the increase in small branches as you zoom in.”

By bridging the gap between art and mathematics, Gao and Newberry endeavored to make their study as approachable as feasible for individuals from both domains and beyond. Its mathematical intricacy reaches a peak with the renowned—or notoriously, depending on your feelings about middle school geometry—Pythagorean theorem: a² + b² = c².

In a broad sense, a and b can be seen as the diameter of smaller branches originating from a larger branch with diameter c. The exponent 2 corresponds to the branch diameter scaling exponent, but for actual trees, its value can range from approximately 1.5 to 3.

The researchers discovered that, in artistic creations where this factor was preserved, observers could readily recognize trees—even when stripped of other identifying features.

Artistic exploration

In their research, Gao and Newberry examined artworks from various regions globally, including 16th-century stone window carvings from the Sidi Saiyyed Mosque in India, an 18th-century artwork titled “Cherry Blossoms” by Japanese artist Matsumuara Goshun, and two early 20th-century creations by Dutch painter Piet Mondrian.

The mosque carvings in India served as the initial inspiration for the research. Despite their highly stylized, serpentine-like branches, these trees possess a captivating, organic sense of proportion, Newberry noted. This led him to ponder if there could be a more universal aspect in how we identify trees. The investigators drew from DaVinci’s study of trees to realize that branch thickness was a significant factor.

Analyzing the branch diameter scaling factor, Gao and Newberry uncovered that several of the carvings exhibited values closer to actual trees than the tree depicted in “Cherry Blossoms,” which appears more organic.

“That was actually quite astonishing for me because Goshun’s painting is more authentic,” Gao remarked.

Newberry echoed that thought and theorized that a more genuine branch diameter scaling factor permits artists to depict trees in more imaginative ways while still maintaining their appearance as trees.

“As you abstract further from details and still desire viewers to recognize this as a lovely tree, you may need to stay closer to reality in other elements,” Newberry explained.

Mondrian’s creations offered a fortunate opportunity to evaluate this theory. He painted a series of artworks representing the same tree, progressively in more abstract forms. In his 1911 piece “De grijze boom” (“The gray tree”), Mondrian had reached a stage in the series where he depicted the tree using merely a collection of black lines against a gray canvas.

“If you show this artwork to anyone, it’s unmistakably a tree,” Newberry observed. “Yet, it lacks color, leaves, and even real branching.”

The researchers discovered that Mondrian’s branch scaling exponent fell within the range of real trees at 2.8. However, for Mondrian’s 1912 “Bloeiende appelboom” (“Blooming apple tree”), that scaling was absent, as was the agreement that the object represented a tree.

“People see dancers, fish scales, water, boats—all sorts of things,” Newberry stated. “The sole distinction between these two artworks—they’re both black strokes on essentially a gray canvas—is whether there exists branch diameter scaling.”

Gao orchestrated the study and evaluated the initial trees as part of her U-M Math Research Experience for Undergraduates project, which was backed by the James Van Loo Applied Mathematics and Physics Undergraduate Support Fund. Newberry engaged in the project as a junior fellow of the Michigan Society of Fellows. Both researchers acknowledged the crucial role that interdisciplinary environments at Michigan played in their investigation.

“We could not have conducted this research without collaboration between the Center for the Study of Complex Systems and the math department. This center is a unique aspect of U of M, where mathematics thrives as a shared language to communicate across disciplinary boundaries,” Newberry expressed. “Additionally, I have been greatly inspired by discussions that brought together mathematicians and art historians at the same table as a part of the Society of Fellows.”